SAT Math 기출문제 유형 분석

SAT Math 시험 준비에 있어 가장 중요한 첫 단계는 문제 유형을 체계적으로 이해하는 것입니다. 단순히 문제를 풀어보는 것을 넘어, 문제의 구조와 패턴을 명확히 파악해야 합니다.

그런 의미에서 SAT Math 문제는 1차원 문제(1D type)와 2차원 문제(2D type)로 나눌 수 있습니다. 문제 해결 과정의 '차원'을 기준으로 분류하면 내가 개념 이해가 부족한지, 아니면 문제의 정보를 해석하고 변환하는 능력이 부족한지를 더 명확하게 알 수 있습니다. 특히 SAT Math 기출문제 오답 노트를 작성할 때 특히 도움이 됩니다.

Domain, Dimension, Skill, Concept 각각으로 문제를 분석해 나가면 지금 SAT Math 고득점을 위해 무엇을 공부해야 하는지 명확하게 파악할 수 있습니다.

• Domain : Algebra, Advanced math, Geometry and Trigonometry, Problem-Solving and Data Analysis → 4개
• Dimension : 1D, 2D → 2개
• Skill : Linear equations in one variable, Linear functions 등 → 19개
• Concept : (SAT Math를 위해 공부해야할 총 Concept list가 궁금하면 아래 카카오톡 문의하기를 누르세요)

SAT Math 1D type

SAT Math 1D 문제는 수학적 개념을 단일 형식으로 제시합니다. 구체적으로 다음 네 가지 형식 중 하나로 문제가 주어집니다.

• Expreesion 표현식
• Equation 방정식
• Graph 그래프
• Image 이미지

핵심은 각 형식에서 직접적으로 문제를 해결해야 한다는 점입니다. 추가적인 형식 변환 없이 주어진 형태의 수학적 개념을 즉시 적용해야 합니다. 형식 별 문제는 SAT Math practice test문제로 보여드리겠습니다.

중요한 학습 포인트: 해당 문제 유형을 성공적으로 풀기 위해서는 해당 수학적 개념에 대한 깊이 있는 이해가 필수적입니다. 개념을 제대로 이해하지 못하면 문제 해결이 근본적으로 불가능합니다.

Expression

문제에서 주어진 식을 정리하면 됩니다.

Equation

방정식을 풀기 위해 필요한 개념을 이용해서 문제를 됩니다.

Graph

그래프에서 파악할 수 있는 정보를 가지고 답을 구하면 됩니다.

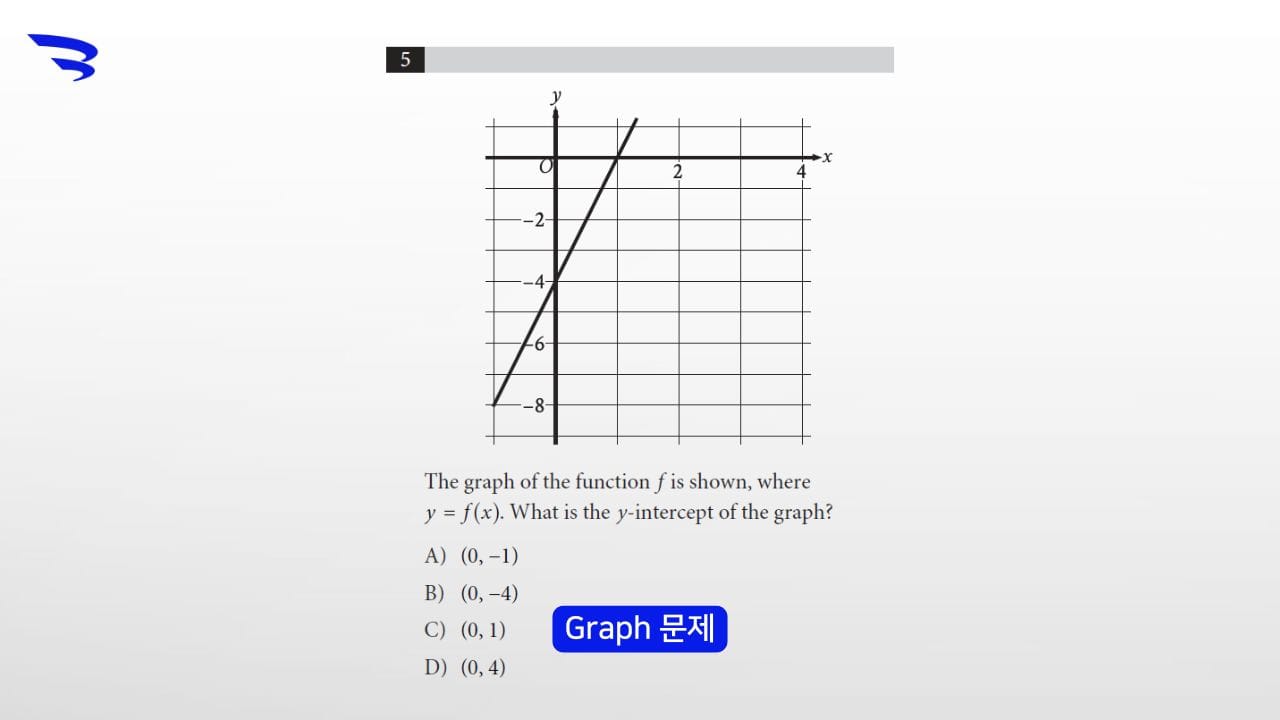
Image

그림을 보고 문제를 풀면 됩니다.

SAT Math 2D type

2차원 문제 유형은 SAT Math에서 더욱 높은 수학적 사고력을 요구하는 문제 유형입니다. 이 유형의 핵심 특징은 문제 해결을 위해 형식 변환(X to Y)이 필수적이라는 점입니다.

2D 문제의 구성 요소

2차원 문제는 1차원 문제의 요소들(Expression, Equation, Graph, Image)에 Word(텍스트) 요소가 추가된 복합적인 구조를 가집니다

• Expression
• Equation
• Graph
• Image
• Word

형식 변환(X to Y)의 특징

• 다중 변환 가능성: 단일 문제 내에서 여러 번의 형식 변환이 요구될 수 있습니다.
• 변환 과정의 복잡성: 각 변환 단계마다 고유의 수학적 접근 방식이 필요합니다.
• 종합적 사고력 요구: 단순 계산을 넘어 다차원적 사고와 분석 능력이 중요합니다.

여기선 대표적 X to Y인 Word to Equation/Equation to Word, Word to Graph/Graph to Word 형식 별 문제를 SAT Math practice test 문제로 보여드리겠습니다.

1. Word to Equation, Equation to Word

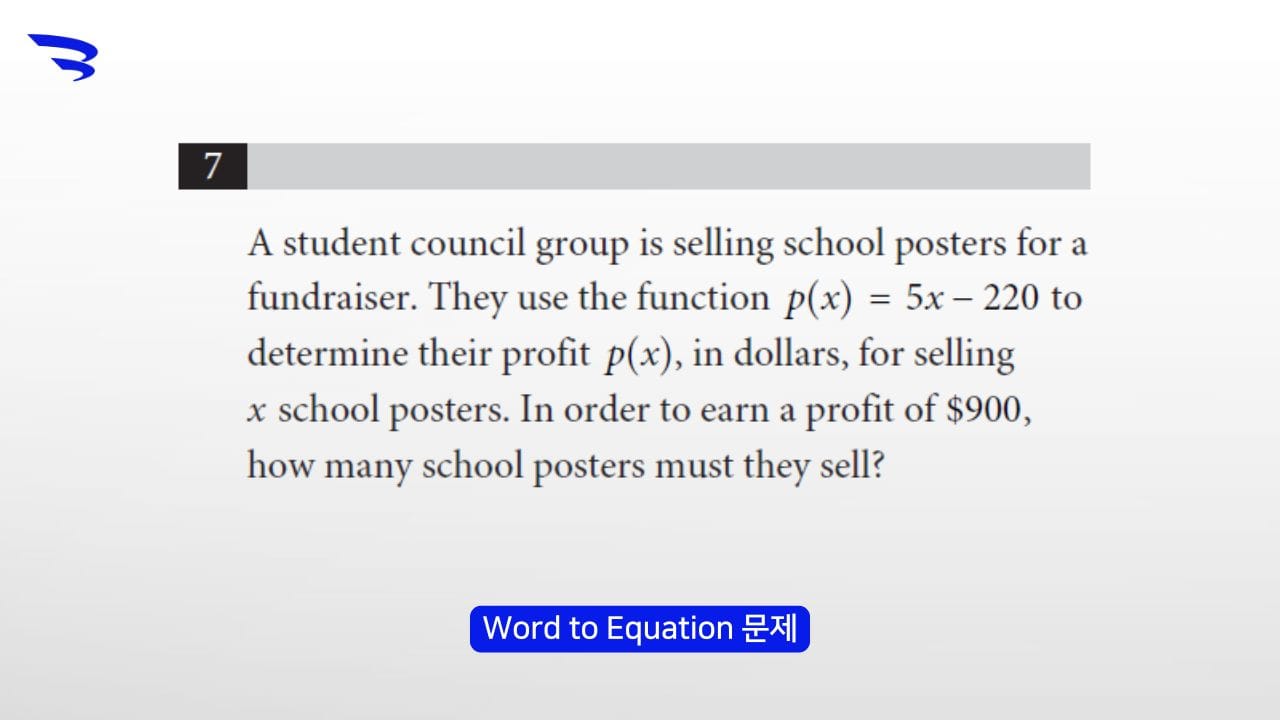
• SAT Math 문제의 상당 부분이 바로 Word to Equation 유형입니다. 예를 들어, 비용 및 수량과 관련된 단어 문제, 나이 관계, 그리고 운동과 관련된 내용을 방정식으로 정리한 뒤에 구하라고 하는 값을 구해야 합니다. 문제에서 요구하는 상황을 정확하게 방정식으로 바꾸는 것이 올바른 문제 해결의 기초입니다. 이 단계에서의 오류는 방정식이 올바르게 풀리더라도 오답으로 이어질 수 있습니다.
• 반대로 방정식을 주고 이 식을 제대로 이해했는지 묻는 문제도 자주 출제됩니다.

2. Word to Graph, Graph to Word

• 문제에 주어진 정보를 그래프를 사용하여 시각적으로 표현하는 유형입니다. 점을 찍거나, 설명에 따라 선이나 곡선을 스케치하거나, 시나리오를 나타내는 올바른 그래프를 선택하는 것이 포함될 수 있습니다.
• 그래프를 주고, 이 그래프를 제대로 해석하는지 묻는 문제도 나옵니다. 다양한 유형의 그래프와 독립 변수와 종속 변수의 관계를 묻는 경우가 많습니다. 개기울기의 의미를 묻거나 특정한 좌표가 의미하는 바를 묻기도 합니다.

효과적인 SAT Math 학습

1차원 문제에서 "개념 적용"은 문제 해결을 위해 필요한 수학적 개념을 떠올리고 직접 적용하는 과정입니다. 2차원 문제에서는 X에서 Y로의 변환 과정 자체가 "개념 적용"의 핵심입니다.

여기서 학습의 중요한 원칙이 있습니다.

• 1차원 문제에서 개념 적용이 미숙한 학생은 2차원 문제에서도 성공할 수 없습니다.
• 많은 문제집이나 초보 강사들이 잘못된 접근을 하고 있습니다.

많은 경우, 강사들은 단순히 같은 개념이 사용된다는 이유로 1차원과 2차원 문제를 동시에 제시합니다. 이는 치명적인 실수입니다. 이렇게 문제를 풀면 학생들은 개념을 제대로 숙지하지도 못하고 문제 풀이법도 제대로 익히지 못합니다. 지금 많은 문제를 풀고 있음에도 SAT 성적이 오르지 않는다면, 바로 이러한 학습 방법의 오류일 가능성이 높습니다.

올바른 학습 전략은 단계적 학습하는 것입니다.

1. 1차원 문제에서 개념 적용 방법을 철저히 익힙니다.
2. 해당 개념에 대한 확실한 이해와 적용 능력을 확보합니다.
3. 충분한 연습 후 2차원 문제로 점진적으로 이동합니다.

기억하세요. 1차원과 2차원 문제를 명확히 구분하고, 단계적으로 학습하는 것이 SAT Math 성공의 열쇠입니다.