3월 SAT 시험 대비 출제 예상 개념 Math(1편)

SAT 시험을 준비하는 학생이라면, Math 섹션에서 중요한 개념을 철저히 익히는 것이 필수입니다. 특히 3월 SAT 시험을 일주일 앞두고 있는 지금, 어떤 개념을 집중적으로 공부해야 할지 고민이 많을 것입니다. 이번 시리즈에서는 최근 공개된 SAT Practice Test 7~10 분석을 통해 3월 SAT 시험에서 출제될 가능성이 높은 핵심 수학 개념을 차례대로 소개해드리겠습니다.

SAT Practice Test 7에서 주목해야 할 문제

이번에 새롭게 공개된 문제 세트가 중요하다는 것은 모두 알고 계실 것이라 생각합니다. 여러 문제들 중에서 저는 이 문제가 가장 먼저 눈에 확 들어왔습니다.

이 문제를 풀기 위해서는 sin과 cos의 관계를 정확히 이해해야 합니다.

• A+B=90° 라면 → sinA=cosB

이 개념을 알고 있다면 이 문제는 10초 만에 해결할 수 있는 문제입니다. 왜냐하면 문제에서는 sin24°, cos66°, cos24°, sin66°가 나오고 있습니다. 그런데 우리가 위 개념을 알고 있다면

sin24°=cos66°
cos24°=sin66°

인 것을 알 수 있기 때문입니다.

이 SAT문제를 주목하는 이유가 무엇인가요?

CollegeBoard의 Questionbank에 있는 Geometry and Trigonometry 195문제 중 sin과 cos의 관계를 묻는 문제는 단 한 문제뿐입니다. 그런데 이 개념이 SAT Practice Test 7에서 등장했을 뿐만 아니라, Practice Test 10에서도 동일한 개념이 출제되었습니다.

Practice Test 9에서는 이 개념을 직접적으로 묻지는 않았지만, 변형이 가능한 형태로 출제되었습니다.

• 이 문제는 닮은 삼각형의 sin값을 묻고 있습니다.
• 만약 cos(L)을 물어보면, 앞서 설명한 문제들과 동일한 개념을 묻는 문제가 됩니다.

Questionbank에서는 이 개념이 더 심화된 형태로 출제되었습니다.

• 그림에 표시되지 않은 점 W를 이용해 각RSW와 각WST의 관계에서 sin과 cos의 관계 개념을 찾아내야 하는 문제입니다.
• 문제에서 지시하는 대로 점 W를 선분 RT 위에 표시하면 ∠RSW와 ∠WST의 합이 90도임을 알 수 있고, sin과 cos의 관계를 활용해 풀 수 있습니다.

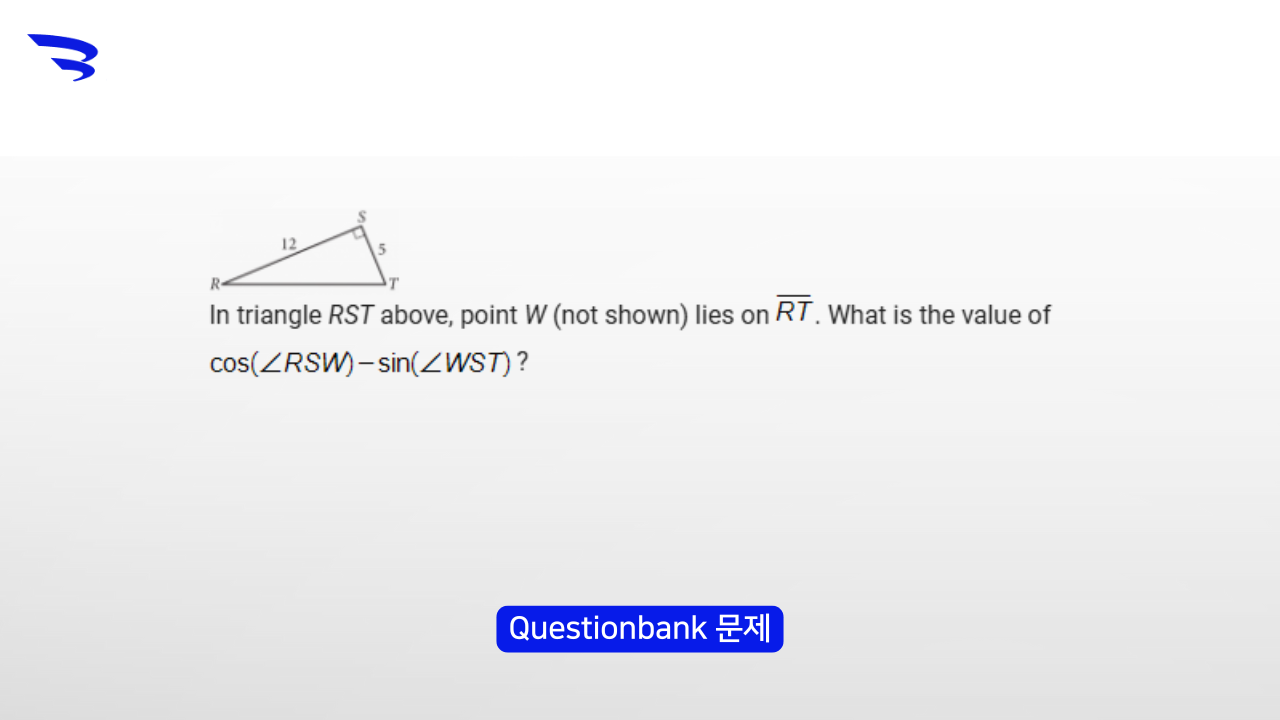
수업을 해보면 이 문제에서 대다수의 학생들은

그림에 w가 없는데, 이걸 어떻게 시작해야 해요?

라고 물어봅니다. 하지만 문제에서 시키는 대로 점 w를 선분 RT의 어딘가에 찍으면 이제 sin과 cos의 관계를 이용하여 답을 구할 수 있습니다. 물론 이 개념을 모른다면, 높은 확률로 '각도를 모르는데 sin, cos값을 어떻게 구하지? 계산기 써야 하나?'라고 생각할 가능성이 높습니다.

3월 SAT 시험 추가 출제 예상 개념: tan의 관계

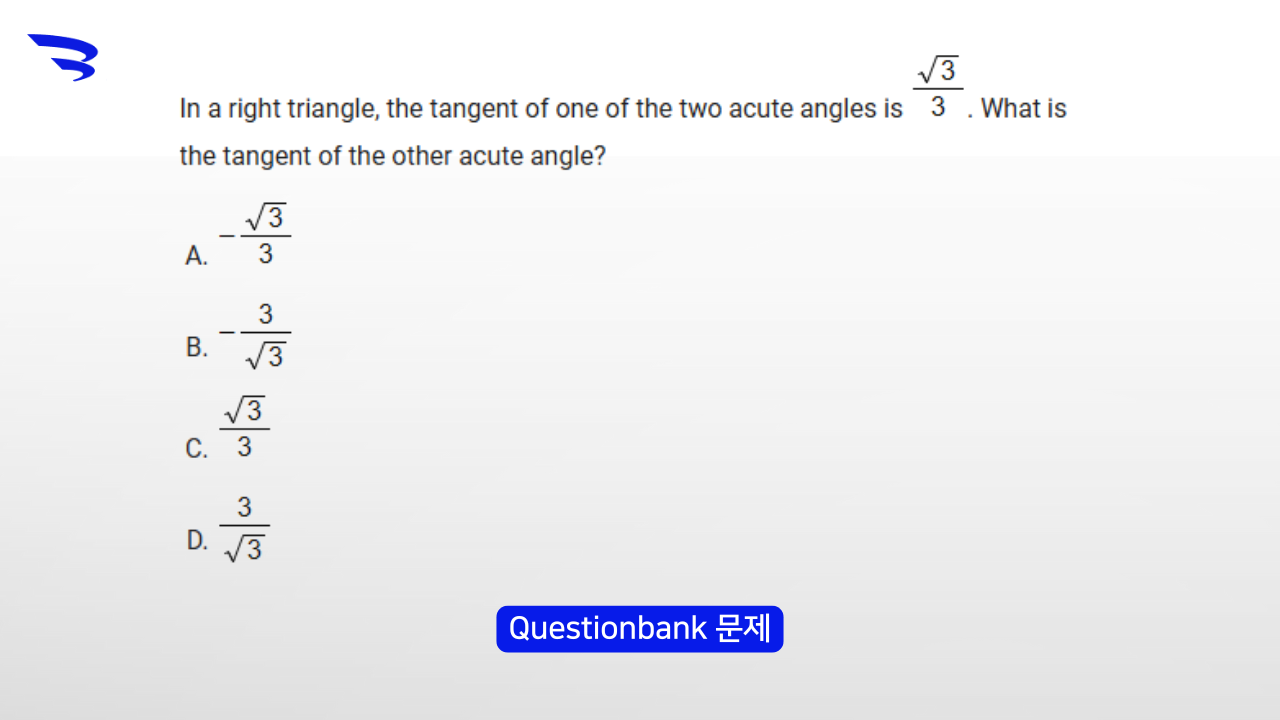
A+B=90°일 때, tanA와 tanB의 관계에 대해 묻는 문제가 3월 SAT시험에 나올 확률을 제게 묻는다면, 20% 이하로 보겠습니다. 하지만 이걸 알아둘 가치가 있냐 없냐고 묻는다면 200% 알아둘 가치가 있다고 생각합니다. 일단 Questionbank에 출제가 된 적이 있습니다. 195개의 Geometry and Trigonometry 문제 중 한 문제가 바로 이 개념을 묻는 문제였습니다.

• A+B=90° 라면 → tanA × tanB=1

직각삼각형 삼각함수의 핵심 관계 정리

직각삼각형에서 직각이 아닌 두 각 A, B가 있다면(A+B=90°):

• sin A = cos B
• tan A × tan B = 1

이 두 가지 개념을 이용한 문제가 3월 SAT시험에 나올 수 있으니 알아두도록 하세요.

위에서 살펴본 6개 문제에 대한 변형 문제 1세트(20문제)를 풀어보고 싶으시다면 댓글에 "1600 + 이메일"을 남겨주세요. 무료로 자료를 보내드립니다.