SAT수학 문제 출제자의 의도 분석하기

SAT수학 문제는 단순한 수학 문제가 아닙니다. 출제자의 의도를 정확히 이해하면 높은 점수를 얻을 수 있는 섬세하게 만들어진 문제입니다. 많은 학생들이 SAT수학 문제에서 어려움을 겪는 이유는 문제의 의도를 제대로 파악하지 못한 상태에서 그냥 문제만 많이 풀면 된다고 생각하는 막연한 학습을 하기 때문입니다.

SAT수학 문제, 어떻게 접근해야 할까?

출제자 의도 분석의 중요성은 두 가지를 꼽을 수 있습니다.

• 명확한 방향성: 출제자의 의도를 이해하면 공부의 방향을 정확히 잡을 수 있습니다.
• 효율적인 학습: 문제의 의도를 파악하면 어떤 부분을 집중적으로 대비해야 할지 계획을 세울 수 있습니다.

SAT Practice test7의 모듈2 21번 문제는 출제자의 의도를 완벽하게 보여주는 좋은 예입니다. 이 문제를 통해 SAT수학 문제의 깊이 있는 접근 방식을 배울 수 있습니다.

차근차근히 살펴보겠습니다.

Word to Image

A line intersects two parallel lines, forming four acute angles and four obtuse angles.

출제자 의도1

이 문장를 보고 아래 그림을 그릴 수 있나요?

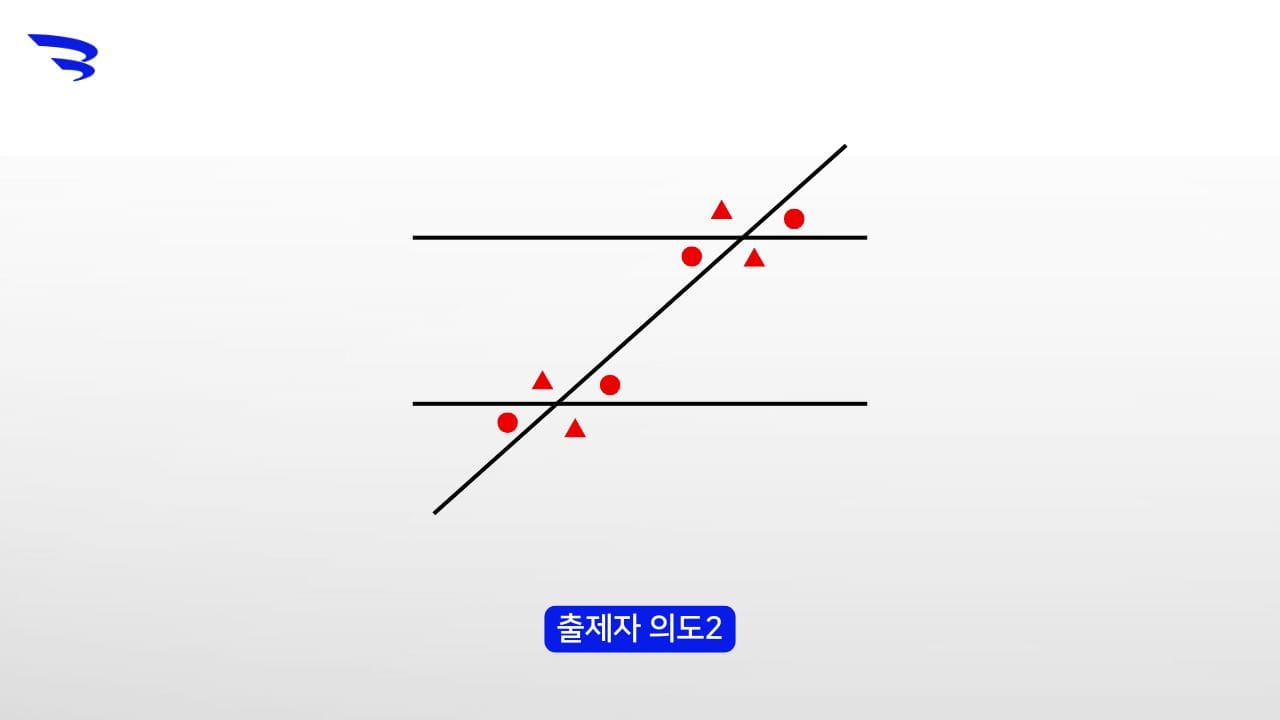
출제자 의도2

vertical angles(맞꼭지각)과 alternate angles(엇각)을 알아서 이 그림에 다음 정보를 추가할 수 있나요?

Word to expression

The measure of one of the acute angles is (9x − 560) °. The sum of the measures of one of the acute angles and three of the obtuse angles is (−18x + w) °.

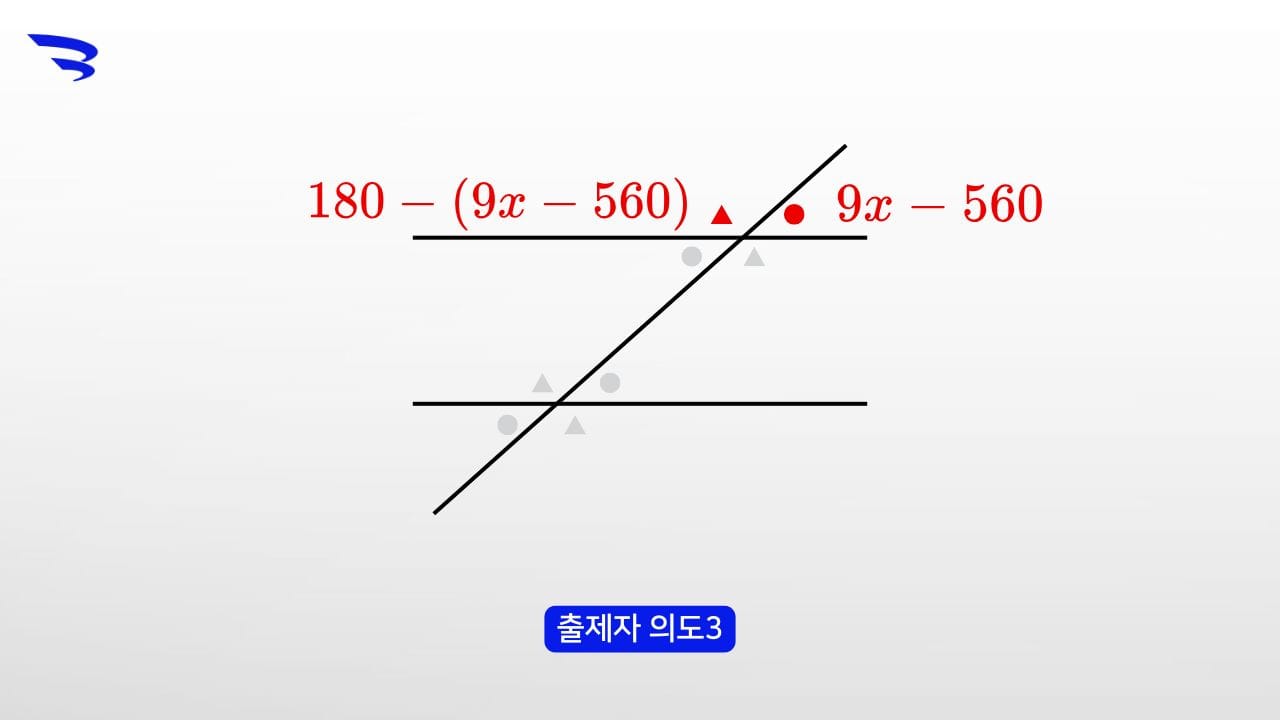
출제자 의도3

이 두 문장을 보고 obtuse angle을 x가 포함된 식으로 표현할 수 있나요?

Word to equation

The sum of the measures of one of the acute angles and three of the obtuse angles is (−18x + w) °.

출제자 의도4

w를 구하기 위해서 아래와 같은 equation을 쓸 수 있나요?

• 9x-560+3(740-9x)=-18x+w

이 네 가지 출제자 의도를 통해 우리가 이 문제를 맞추기 위해 알아야 할 개념은 4가지입니다.

• vertical angles(맞꼭지각)
• alternate angles(엇각)
• Straight angle(직선각)
• Solving Linear Equations

결론

word to X와 네 가지 개념을 알고 있지 못한다면 이 문제를 맞출 수 없습니다. 만약 word to X와 vertical angles(맞꼭지각), alternate angles(엇각), Straight angle(직선각), Solving Linear Equations가 부족해서 해당 개념에 대한 설명 강의가 필요하거나 문제를 풀어보고 싶다면 카카오톡으로 연락주세요.

저희 카톡방은 언제나 열려있습니다.